Example continued...
Tom is at rest with respect to the train whereas Peter and the train are moving with respect to each other. Knowing Peter's measurement of the train's length, determine what Tom's measurement of the train's length is? And according to Tom, how much time does it take the train to pass Peter?
Knowing Peterís measurement of
the trainís length we can determine Tomís measurement of the trainís
length where LT is the length of the train
LTrest(T) = LTmove(P)
[1-(v/c)2]-1/2 =
60 [1- (0.8)2]-1/2 = 100 meters
Tom measures the trainís length
at 100 meters.
According to Tom it takes 4.17 X 10-7
seconds for the train to pass Peter (time = distance/velocity)
Given Peter's measurement of the length of the platform, determine the length of the platform as measured by Tom.
Given Peterís measurement for the length of the platform we can determine what length Tom would measure for the platform where LP is the length of the platform. You'll notice that the positions of LPrest and LPmove were switched. The reason this works is because the second half of the formula is no longer to the power of (-1/2) but (+1/2)
LPmove(T) = LPrest(P)
[1-(v/c)2]1/2 =
60 [1- (0.8)2]1/2 = 36 meters
Tom would
measure the platform to be 36 meters long.
As we have observed, each personís observations of the length of the train and the platform are very different from each otherís. This is due to Einsteinís theory of special relativity. The same concepts can be applied to time.
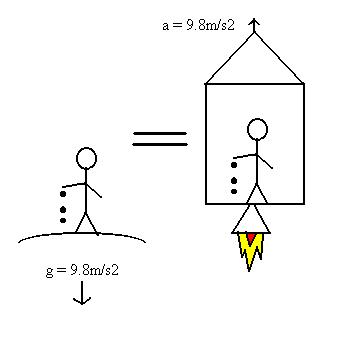
What happens when you are accelerating? Einstein answers this question where he relates acceleration due to gravity and acceleration in free space. Einstein says that the acceleration due to gravity can be recreated in free space by accelerating the surroundings of an object, i.e. spaceship, at the same acceleration caused by gravity. According to Einstein, all experiments, whether in free space accelerating or on earth will give the same results. This principle is called the Weak Equivalence Principle. If the acceleration in free space is twice that of the acceleration of gravity on earth, then the force experienced in the free space will be twice that of which is experienced on earth, thus, twice the acceleration will produce 2 g-forces where 1 g-force is equivalent to the force of gravity on earth (9.81m/s2).